Full Adder
Contents
ToggleA full adder is the powerhouse digital circuit that adds three binary bits—two inputs (A, B) plus a carry-in (Cin) from previous addition—to produce a sum (S) and carry-out (Cout). Built from two half adders and an OR gate (or 2 XORs, 2 ANDs, 1 OR), it’s the heart of every CPU’s ALU for multi-bit arithmetic.
Think of it like school addition with borrowing: 1+1+1=11 binary (S=1, Cout=1). Half adders handle pairs; full adders chain them for 64-bit numbers. For COA students, it’s how computers crunch massive calculations instantly. Let’s unpack it step-by-step.
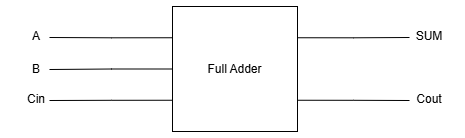
What is a Full Adder?
Full adder is a combinational circuit (no memory, instant outputs) that overcomes half adder’s limit—no Cin handling. It processes A + B + Cin, outputting S = A ⊕ B ⊕ Cin and Cout = AB +Cin(A ⊕ B)
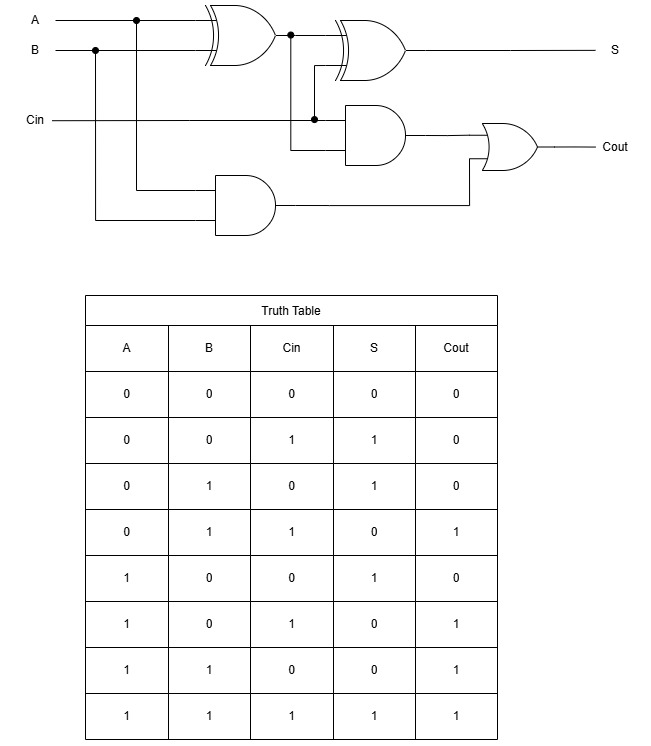
The carry input Cin brings in the carry bit from the previous stage of addition.
When adding binary numbers with more than one bit, each column may generate a carry. That carry must be added to the next column.
Purpose of Full Adder in Digital Systems
Full adders enable complete binary addition across multiple bits by propagating carries. Core purposes:
Arithmetic Core: Powers ALUs for +, -, multiply foundations.
Carry Propagation: Chains LSB to MSB seamlessly.
Scalable Math: Builds 8/16/32/64-bit adders.
In GPUs, they render 4K graphics by pixel math. Without full adders, no spreadsheets, games, or crypto mining.
How Full Adder Works: Step-by-Step
Inputs Hit: A/B data bits, Cin from prior stage.
Half Adder 1: A+B → Sum1 (XOR), Carry1 (AND).
Half Adder 2: Sum1 + Cin → S (XOR), Carry2 (AND).
OR Gate: Carry1 OR Carry2 → Cout (any carry? flag it).
Outputs Fire: Nanosecond propagation.