Identities(Laws) of Boolean Algebra
Contents
ToggleBoolean algebra identities, or laws, provide rules to simplify expressions and minimize logic gates in digital circuits. These fundamental properties like identity, idempotent, and De Morgan’s theorem reduce complex Boolean functions to efficient forms for CPUs and ALUs. Circuit designers use them to shrink smartphone chips, saving power.
What Are Boolean Algebra Identities?
Definition and Role in Digital Design
Identities are equations true for all variables (A=0/1), like A+0=A. They enable algebraic manipulation without truth table verification. In organization, simplify ALU logic for faster execution.
Using Boolean Laws reduces gates (fewer transistors), power, delay. Tools like Espresso automate, but manual mastery aids exams. Ties to registers:- Simplified control logic selects PC/IR faster.
Basic Laws of Boolean Algebra
1. Boolean Addition
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 1
The boolean addition is nothing but logical OR operation.
2. Boolean Multiplication
0 . 0 = 0
0 . 1 = 0
1 . 0 = 0
1 + 1 = 1
The boolean multiplication is nothing but logical AND operation.
There are few more laws that derived from boolean addition and multiplication.
Identity Law –
OR: A + 0 = A
AND: A · 1 = A
Null (Dominance) Law –
OR: A + 1 = 1
AND: A · 0 = 0
Idempotent Law –
OR: A + A = A
AND: A · A = A
Complement Law –
OR: A + A’ = 1
AND: A · A’ = 0
Double negation law ( Involution Law ) –
((A)’)’ = A
3. Commulative Property
According to the Commutative Property, changing the order of the operands in a Boolean expression does not affect the final result. In simple terms, swapping the inputs still get us the same output.
A + B = B + A
(OR operation is commutative)A · B = B · A
(AND operation is also commutative)
This law shows that the sequence of inputs does not matter for AND or OR operations, they produce the same output regardless of order.
4. Associative Property
According to the Associative Property, when three or more variables are combined using the same Boolean operation, the way they are grouped does not change the final result. In other words, rearranging the parentheses does not affect the output.
A + B = B + A
(OR operation is commutative)A · B = B · A
(AND operation is also commutative)
This law shows that the sequence of inputs does not matter for AND or OR operations, they produce the same output regardless of order.
5. Distributive Property
The Distributive Property, shows one Boolean operation can be applied across another. It allows you to expand or factor expressions just like in regular algebra. This law makes it easier to simplify or restructure Boolean equations.
A · (B + C) = A·B + A·C
(AND distributes over OR)A + (B · C) = (A + B)(A + C)
(OR distributes over AND)
This property is especially useful when converting expressions into SOP or POS forms, because it helps break down or combine terms in a systematic way.
6. Absorption Law
A + AB = A
Proof : A + AB
= A.1 + AB
= A(1 + B)
= A.1 = A [ According to Null Law ]
DeMorgan's Theorem
DeMorgan’s theorem states two important laws in boolean algebra. The first theorem states that the complement of a product is equal to the sum of complements.
(A.B)’ = A’ + B’
The second theorem states that the complement of a sum is equal to the product of complements.
(A + B)’ = A’.B’
Minimization (Simplification) of Boolean Expressions using Algebraic method
Let us consider an example of a Boolean function : ABC + ABC’ + A’C
The logic diagram for the Boolean function ABC + ABC’ + A’C :
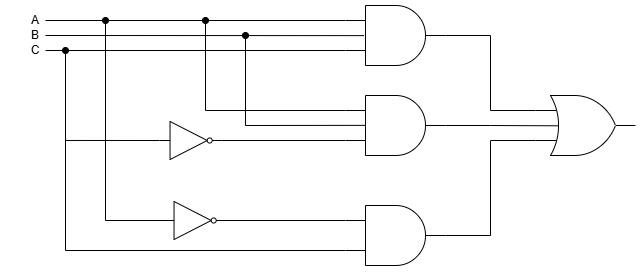
Simplify this Boolean function :
ABC + ABC’ + A’C
AB(C’ + C) + A’C
AB + A’C [ Using Complement Law]
Hence, the simplified Boolean function will be AB + A’C
The logic diagram for Boolean function AB + A’C :
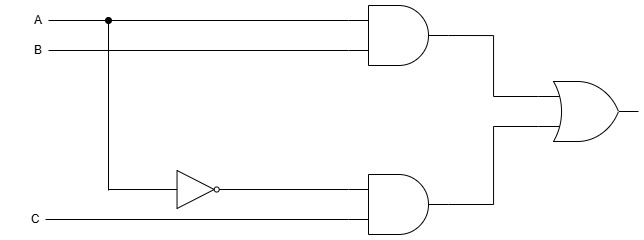
FAQ
What is De Morgan’s Law?
¯(A + B) = ¯A · ¯B—inverts and swaps OR/AND.
Simplest Boolean Identity?
Identity: A + 0 = A.
How Many Boolean Laws Exist?
12 core (basic + advanced).
Example of Absorption Law?
A + A·B = A (A absorbs term).